
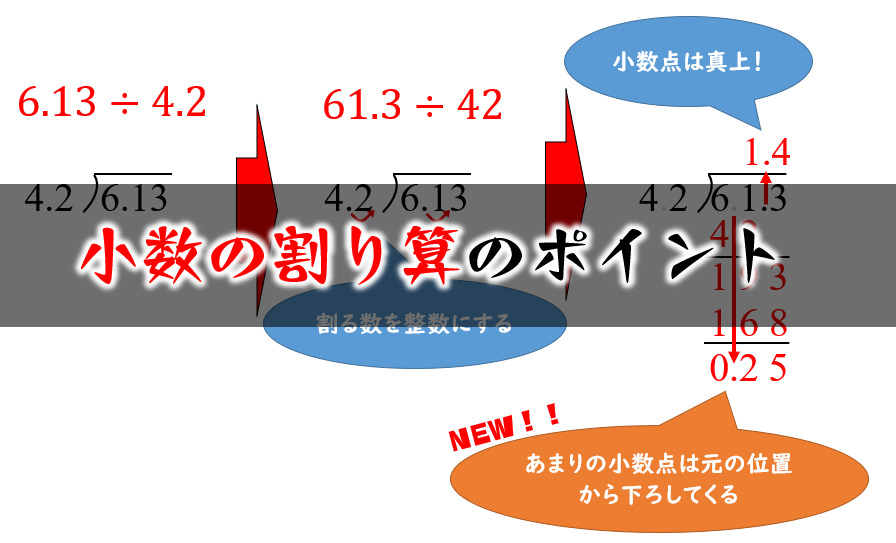
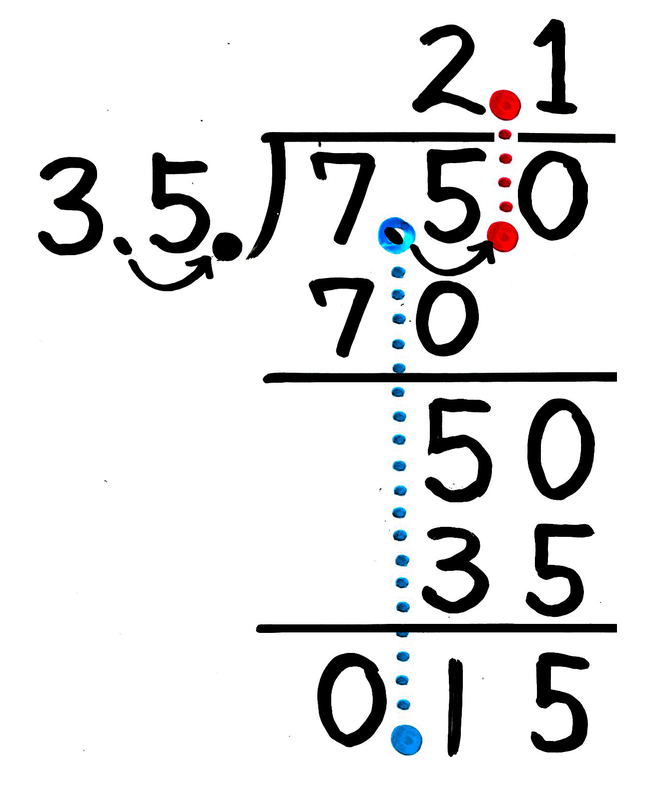
割り算の筆算のやり方
上の構造式を毎回設定して解けばいいので,下に紹介する 剰余の定理は存在を知らなくても大きな問題にはなりません. 剰余の定理 剰余の定理(remainder theorem)とは,整式を1次式で割ったときの余りに関する定理です.About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
余りのある 割り算 教え方
余りのある 割り算 教え方- 余りのある割り算を「÷」で表すときの等号の使い方(意味)について質問します。 23÷7=3あまり2 26÷8=3あまり2 28÷9=3あまり1 となります。 このとき、式「23÷7」と等しいものは「3」か、「3あまり2」のどちらでしょうか。あまりのあるわり算:あまりの活用 学習指導案 (PDF) 通しビデオ (授業) 版 1 著者 笠井さゆり 授業日 14年06月28日 学校名 山梨大学教育人間科学部附属小学校 指導者 笠井さゆり 対象学年 小学校3年生(9 years old) 教科 算数 概要

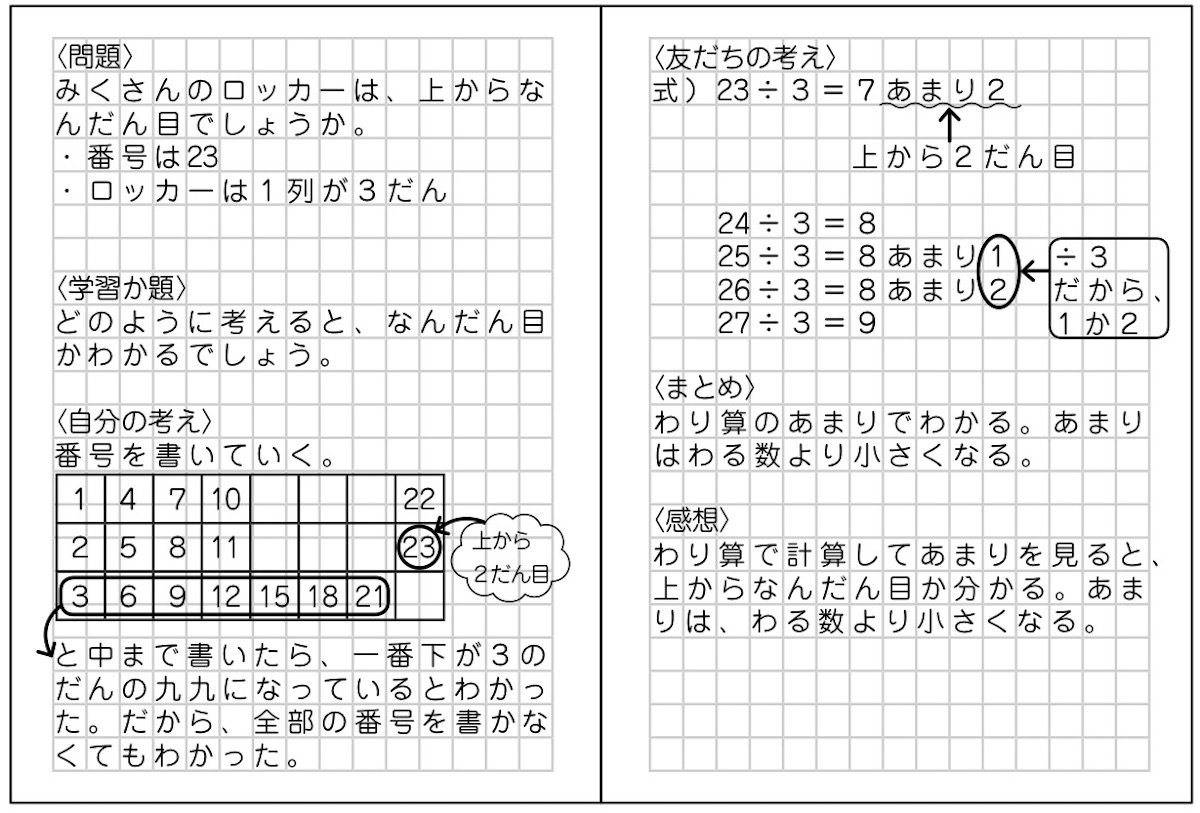
3年算数 あまりのあるわり算 第4時 指導実践報告 あまりはわる数より小さくなる ネコ好きな学校の先生の日常
算数の授業「余りのある割り算」の概要 小学生の授業で使えるスクラッチの簡単なプログラム 簡単にプログラム作成:数字のコスチューム 簡単にプログラム作成:割られる数 簡単にプログラム作成:割る数 簡単にプログラム作成:答え 簡単に・あまりのあるわり算 の式の関係的な見方を 通して,あまりと除数 の大きさの関係を理解 する。 ・ ÷4 の計算について除数とあま りの関係を調べる。 ・(追体験活動)除数5,6,7の場合 のあまりと除数について,類推的に 調べ,その関係をまとめる。 そろばんで余りのある割り算の やり方を教えてください。 娘がそろばん8級をやっていますが、 余りのある割り算のやり方(考え方や玉の置き方)が全く思い出せないようでして・・余りが出ない普通の割り算は 問題なくできるようです。
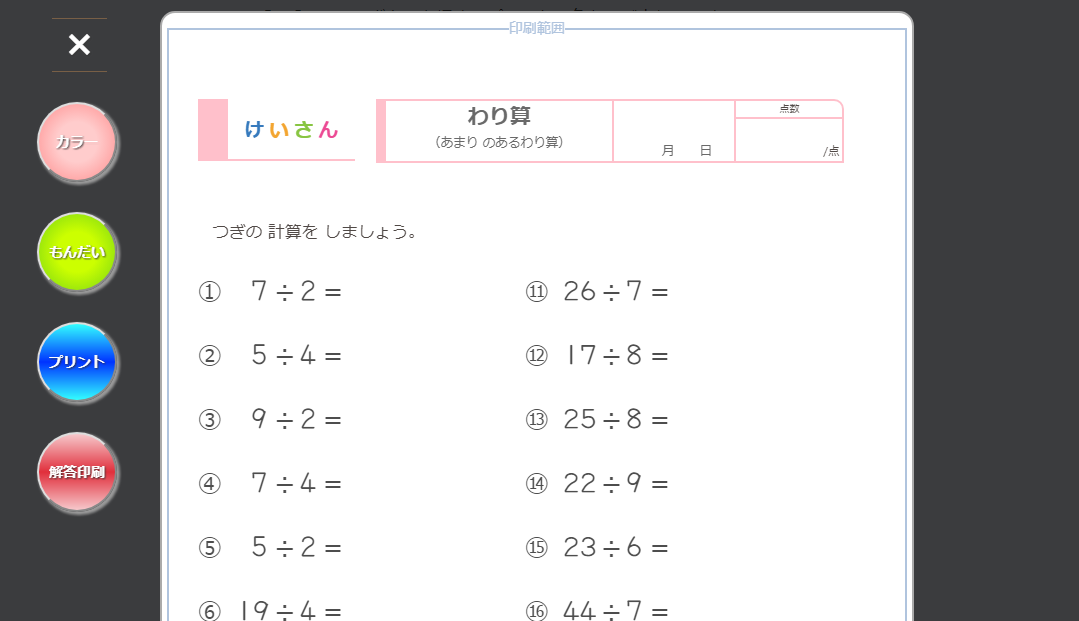
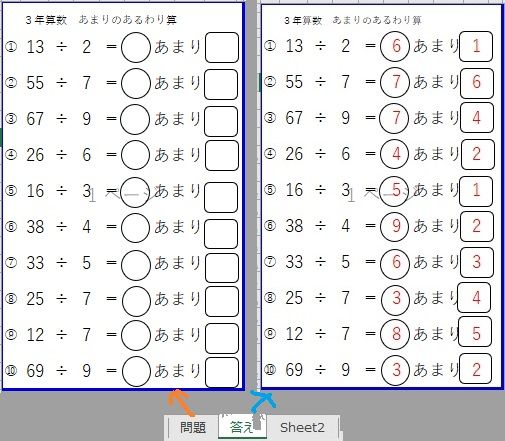
あまりのあるわり算のプリントです。 このプリントを解くには、かけ算だけではなくひき算も使わなければいけません。 今ちょうど学習をする3年生はもちろん、頭の活性化としてそれ以上の学年でも使ってみてはどうでしょうか。 問のプリントと50問また、あまりのあるわり算では、下のように「たしかめ算」をする習慣をつけさせておくと自分で間違いに気づけるようになります。 あまりのあるわり算とたしかめの式 下のような関係があります たとえば 17÷3=5あまり2の場合は division remainder 割り算 = division 余り = 色々な英訳があります。 他の場合で、"excess"か"surplus" (両方「余裕」の意味)が言えますが、数学の余りは"remainder"です。 Remainderだけで十分ですが、division remainderでも間違えません。 しかし、"remainder"のみの方
余りのある 割り算 教え方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 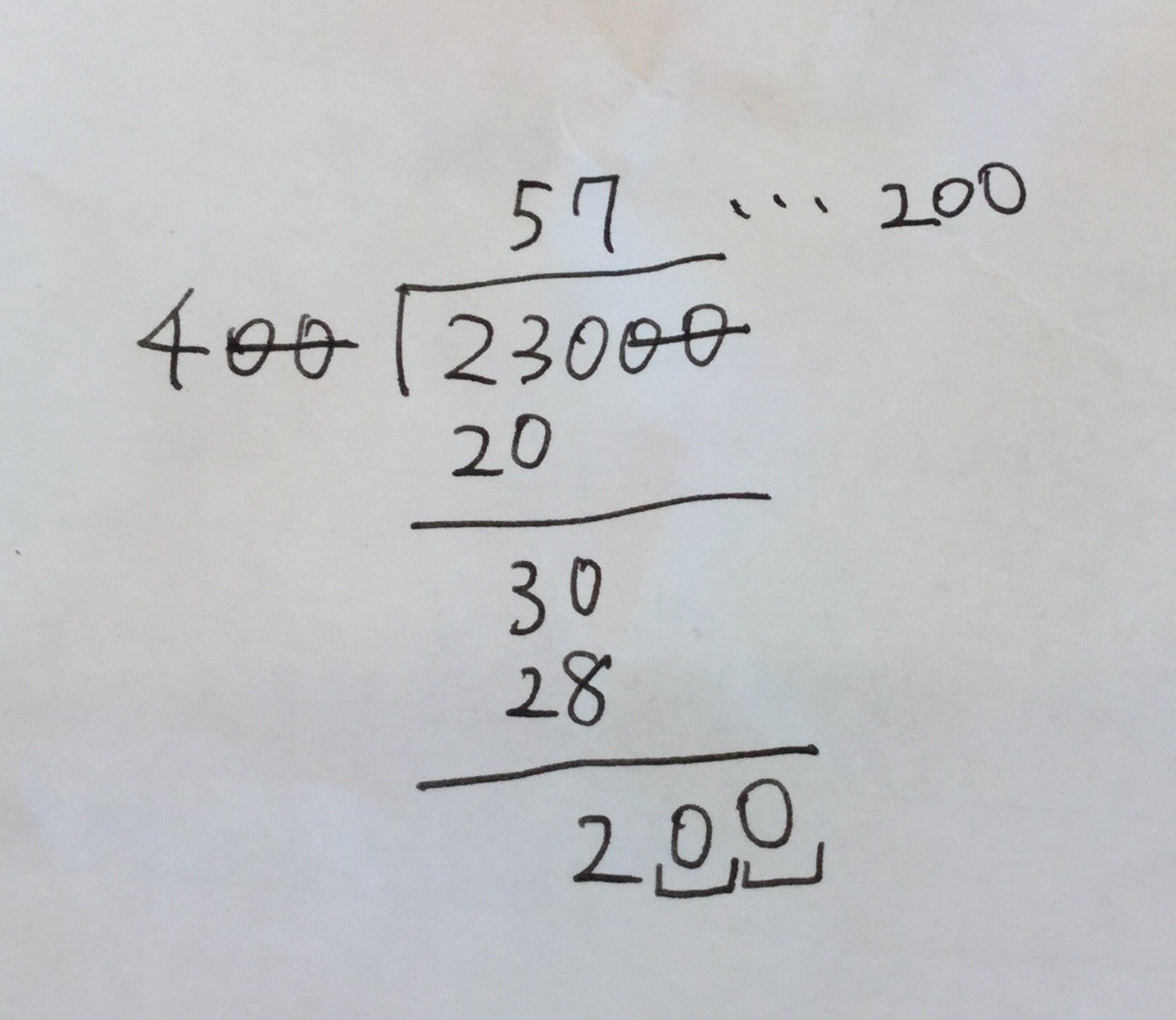 |  |
-(%E7%AD%86%E7%AE%97)%E4%BD%99%E3%82%8A%E3%81%AE%E3%81%82%E3%82%8B%E9%99%A4%E7%AE%97(2%E6%A1%81)-1.png) |  |  |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「余りのある 割り算 教え方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |
HiroPaPaは知りませんでした この表記が変わったのには理由が二つあるそうです。 理由① わり算のたしかめをするときにわかりすくするため 以下のたしかめ式の方が,どの数値をどこにあてはめるかがわかりやすくなるということです 「わる数×商通常の割り算はともかく,余りのある割り算だと急に正答率が悪くなります. 9÷4= のような単純な割り算ならともかく,割る数が小数になったり,あるいは,逆算になったりすると計算のやり方がわからない・・・そのような場面がよくあります.しかし,余りがあろうがなかろうが
Incoming Term: 余りのある 割り算, 余りのある 割り算 プリント, 余りのある 割り算 筆算, 余りのある 割り算 教え方, 余りのある 割り算 文章問題,




0 件のコメント:
コメントを投稿