楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表面積) a ≧ b ≧ c ならば、表面積は楕円積分を用いて次式で与えられる。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、 落ち着いて計算してみよう! 台形の体積の公式がわかる3ステップ むちゃ便利だけど、 なんで公式で計算できちゃうんだろう?平面図形 公式 集 高さ ℓ=弧の長さ S =面積 V =体積 四角柱 (縦×横)×高さ=体積 (a×b) × h = S

中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clear
立体 の 切断 体積 公式
立体 の 切断 体積 公式-ここからは体積を学んでいきたいと思います。体積は表面積と違って簡単です! 公式があるのでしっかり覚えていきましょう!単位が「cm²」ではなく「cm³」なので注意してください。 「柱の体積=底面積×高さ」 で求めることができます。よって立方体の体積=2×2×2=8です。 また、上記の公式をみると「立方体の体積が分かっていれば1辺の長さが逆算できる」と分かります。 例えば立方体の体積=m 3 のとき1辺の長さは約27mです。



Http Www Onomichi Ed Jp Mukaihigashi E D Siryo Kenkyu Sidoanr01 6 2 Pdf
直方体と立方体の体積の求め方を考えます。 1辺が 1 cm の立方体が何個分あるかで求めることができます。 縦×横×高さ=直方体の体積,1辺×1辺×1辺=立方体の体積となります。立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 角柱、円柱、円錐、球、の体積と表面積の公式がややこしくてワケわからなかったので、頭を整理するために1ページにまとめてみました。定期テストが始まるまでトイレに貼っておくために作りました😅 学年 中学1年生, 単元 立体の体積と表面積, キーワード 空間図形,立体,体積,表面積,球
角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 中学1年生で習う空間図形には、様々な立体の体積や表面積の求め方が含まれます。主に柱体(角柱・円柱)、錐体(角錐・円錐)、球の3種類の立体です。体積 = 底面積 × 高さ立体の体積 (V)、表面積 (S)または側面積 (F)および重心位置 (G) 「立体の体積 (V)、表面積 (S)または側面積 (F)および重心位置 (G)」からは、以下の計算がご利用いただけます。 立体の体積 (V)、表面積 (S)または側面積 (F)および重心位置 (G) 単位換算 公式計算
立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)た立体と考えることができます(数学の世界では,円 えん 環 かん 体 たい またはトーラスと呼ばれています)。 円の重心はその中心と一致するので,もとの円の半径と,円の中心と直線との距離がわかれば,ドーナツ形 の体積を求めることができます。




体積の求め方 公式一覧 小学生 中学生の勉強




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。まずは立体の体積を求める公式を確認しましょう。 角柱・円柱 底面積 $\textcolor{blue}{×}$ 高さ 角錐・円錐 底面積 $×$ 高さ $\textcolor{blue}{×\frac{1}{3}}$ 球 $\textcolor{blue}{\frac{4}{3}×π×r^3}$ $3$ 種類の公式を使い、いろいろな立体の体積を求めてみま① 立体のすべての面の面積の和を表面積という。 また,側面全体の面積を側面積,1 つの底面の 面積を底面積という。 ②(柱体の体積)=(底面積)×(高さ),(柱体の表面積)=(側面積)+(底面




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3)公式計算 平面図形の面積(a),周長(l)および重心位置(g) p11 平面図形の性質 p12 立体の体積(v),表面積(s)または側面積(f)および重心位置(g) p12②角柱や円柱の体積の求め方 ③角柱や円柱の体積の公式 ④生活場面での立体の体積を求めるよさ 教え方1 教え方1 5年生で勉強した直方体や立方体の体積の求める公式を生かして、四角柱の体積の求め方を気づかせます。




中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clear




中1数学 立体の体積 練習編 映像授業のtry It トライイット
立方体の体積の求め方公式 サイコロの形をしている立方体は、一辺の長さがどれも同じ。 立方体の体積は、次の公式で求められます。 立方体の体積=1辺×1辺×1辺 直方体の体積の求め方公式 直方体の体積は、次の公式で求められます。V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。上の基本問題をこの公式を使って求める (1) r=5、h=10 だから、V=π ×5 2 ×10=250π cm 3




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
立方体の体積 立方体の体積 立方体の辺の長さから体積と表面積を計算します。 立方体の辺の長さ 立方体の辺の長さ 立方体の体積から辺の長さと表面積を計算します。 直方体の体積 直方体の体積 直方体の三辺の長さから体積と表面積を計算します。 体積=底面積×高さ ここで、そもそも「体積」とは何か考えてみます。 辞書を引くと「立体が占める空間の大きさ」のように書いてありますが、「立体の大きさ」と捕らえておけば問題はないでしょう。 実はこの「体積」の値というものは「比」です。 関連する他の公式 回転体の体積を求める公式はいくつもあります! x = g (y) x=g(y) x = g (y) , y = a y=a y = a , y = b y=b y = b , y y y 軸で囲まれた領域を y y y 軸のまわりに回転させてできる図形の体積は, ∫ a b π {g (y)} 2 d y \displaystyle\int_{a}^b\pi \{g(y)\}^2dy ∫ a b π {g




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
今回は 「立体の体積」 を求めるよ。 体積の求め方は、「すい」と「柱」に関して2つの公式を覚えてしまおう。角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは まずは、平面を垂直に積み重ねて立体の体積を求める公式を確認しましょう。 定積分と体積 \(x\) 軸に垂直な切り口の面積が \(S(x)\) である立体の、\(x = a\) から \(x = b\) \((a < b)\) における体積




体積 表面積




円柱の表面積と体積を求める公式 具体例で学ぶ数学
Junior High数学的数学中2 立体の体積と表面積 公式 筆記 Clear 小5 算数 小5 5 体積の求め方のくふう Youtube 小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生立体の体積&容積および諸数値 V=容積、S=表面積、As=側面積、Ab=底面積、x=底面より重心までの距離 寸 法 容積および諸数値 寸 法 容積および諸数値 V=a 2 S=6a 2 As=4d 2 正多角形 a=辺長三角形の面積の公式から =(5×6÷2)×12=180 答え180 ※上の説明の()の中の高さは三角形の面積の高さで 最後の高さは立体の高さであることに注意しましょう。 教え方4 教え方4 角柱の体積の求め方の考えを使って、円柱の体積の求め方を考えさせます。




円錐の体積ってなんであの公式なの Webty Staff Blog



Http Www Onomichi Ed Jp Mukaihigashi E D Siryo Kenkyu Sidoanr01 6 2 Pdf
③ 公式にあてはめて,円柱の体積を求めましょう。 (式) 答え ( ) 下の図は,立方体と円柱の半分を組み合わせた立体です。 体積を求めましょう。 (式) 答え ( ) 1 3 2 4 10.立体の体積




体積の求め方 計算公式一覧




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
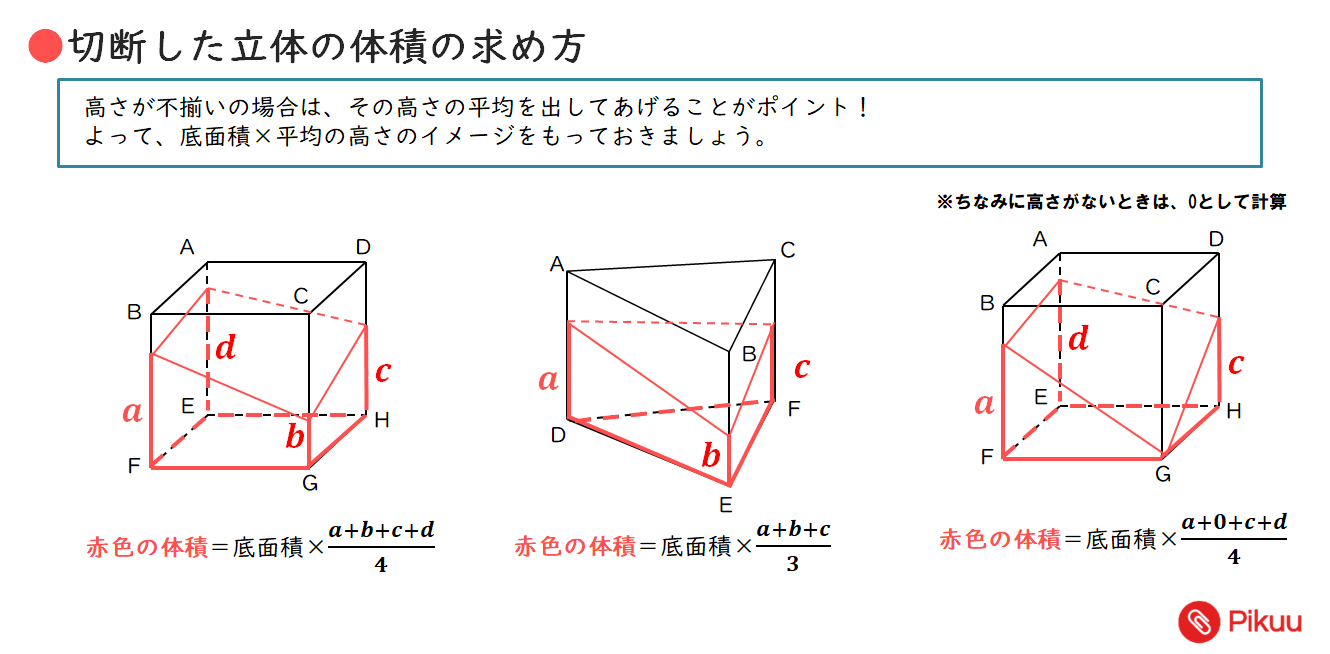



高校入試対策数学 切断した立体の体積を求める練習問題 Pikuu




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




小5 複雑な立体の体積 直方体 日本語版 Youtube




スタディピア 立体の体積
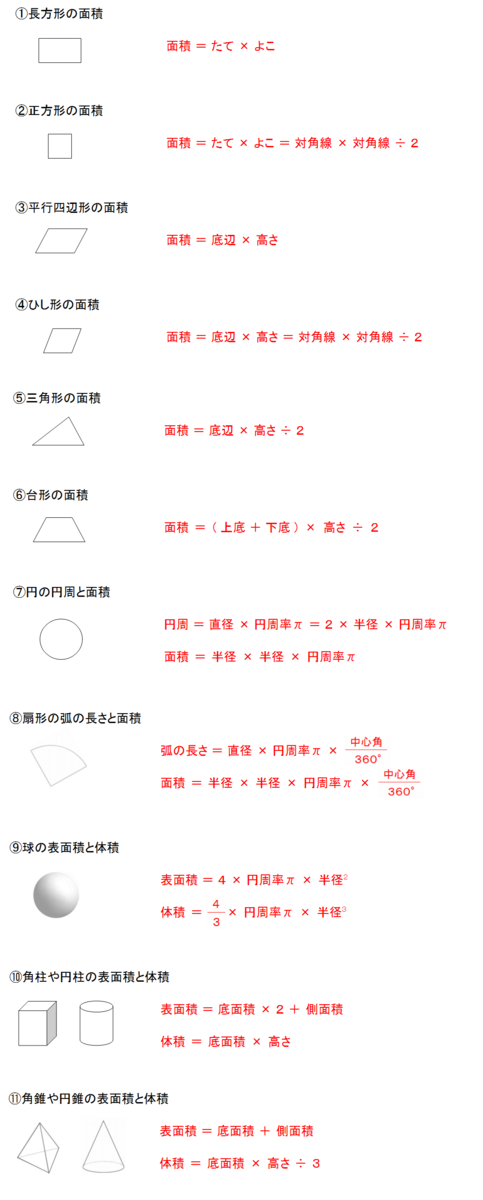



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の体積を求める公式



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



1



立体の体積 テストの前に




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




四角錐台の体積 高精度計算サイト



立派な 台形 体積 求め 方




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




中1 数学 中1 立体の表面積 Youtube




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




球の体積と表面積 公式と計算問題と証明 Irohabook
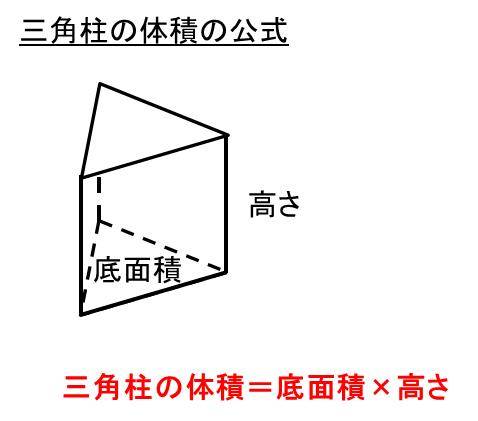



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム
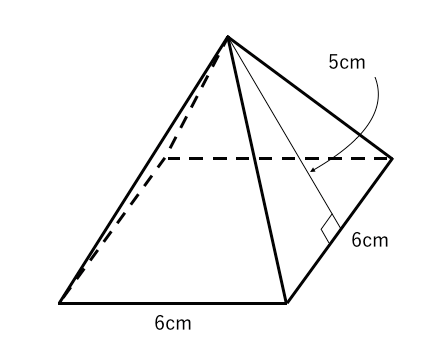



立体の表面積を求める 練習問題 苦手な数学を簡単に




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




公式を図解 すい体の体積 円すいの表面積の求め方




体積の求め方 計算公式一覧



1
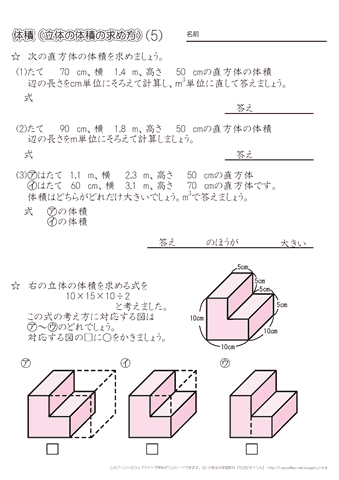



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
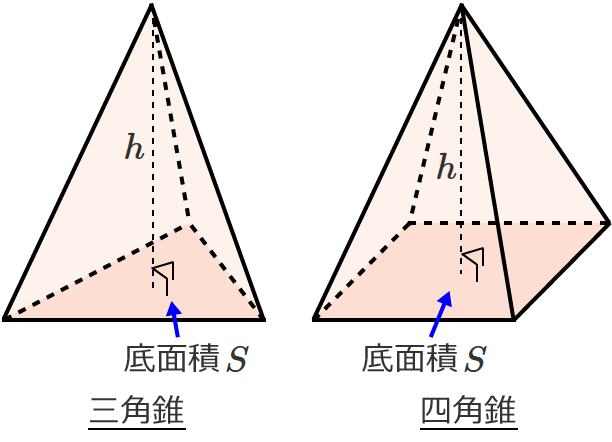



立体の体積を求める公式




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
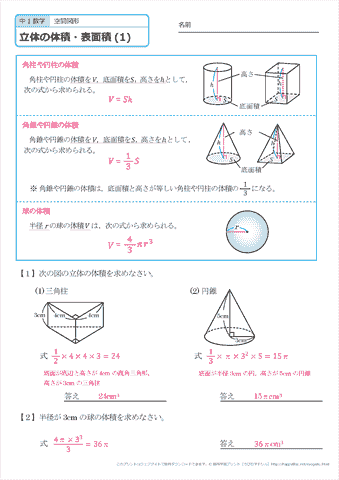



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clear




体積の求め方 計算公式一覧




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
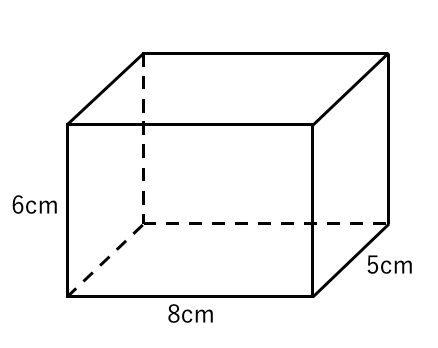



立体の体積を求める 苦手な数学を簡単に




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座
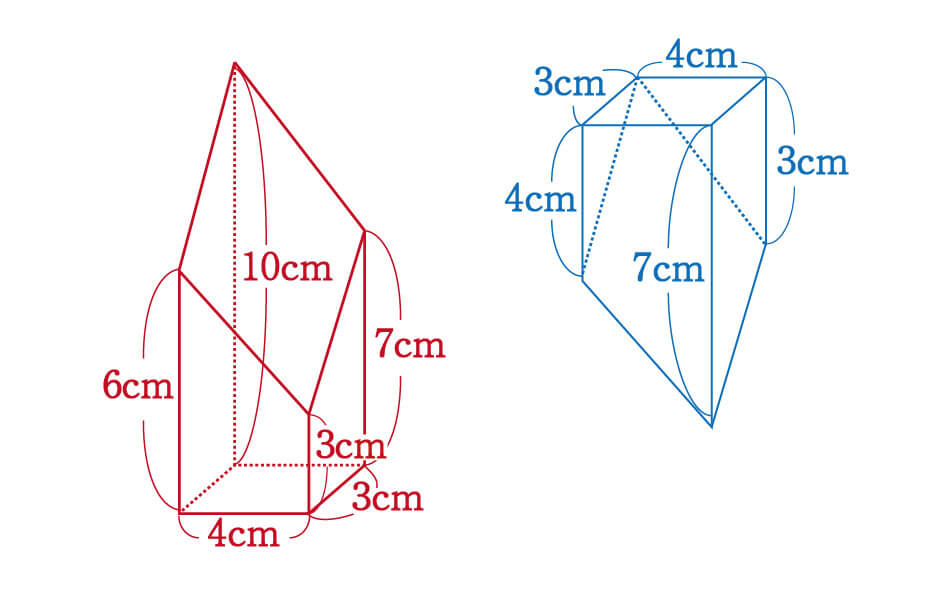



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




公式を図解 すい体の体積 円すいの表面積の求め方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
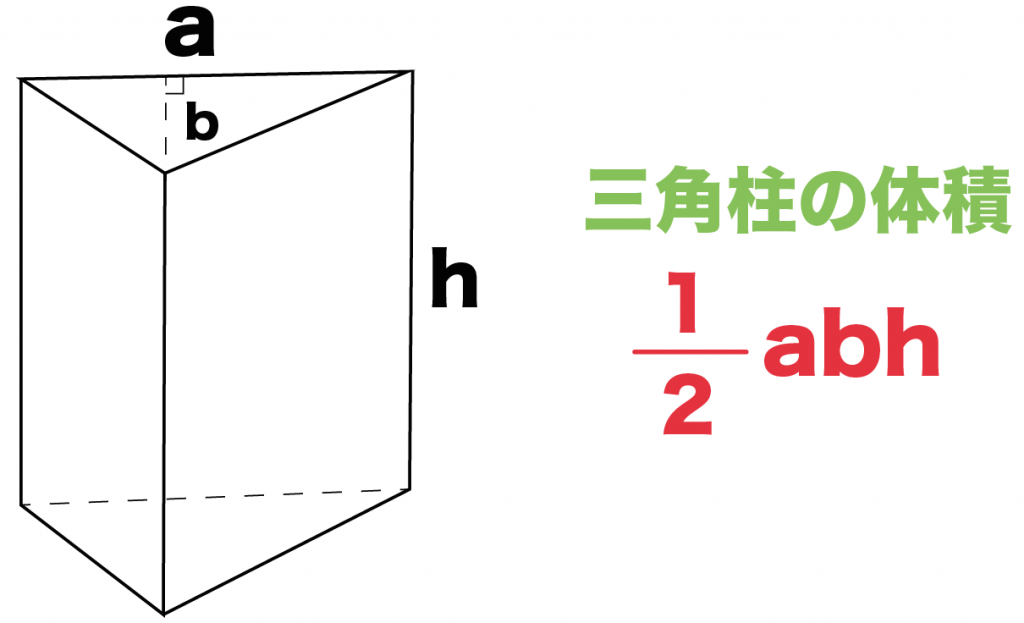



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



1
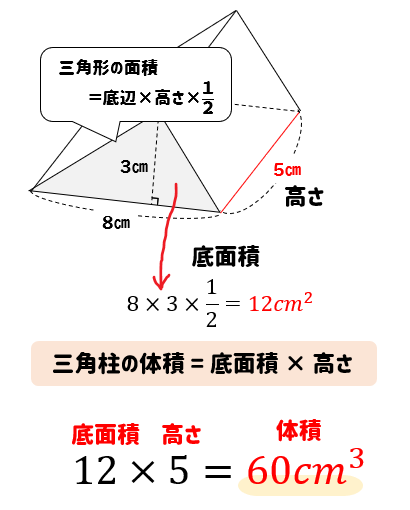



3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




中1 数学 中1 立体の体積 Youtube



6年算数立体の体積その2 教え方




小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 小学校 算数 学習




空間図形14 円すい台の体積 Youtube




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




6年算数立体の体積1 教え方




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




円錐の体積ってなんであの公式なの Webty Staff Blog
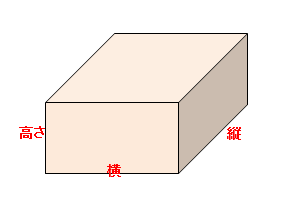



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー



Q Tbn And9gcrcfjh5dnkywzu1xman7gtxgd Ehtkomy4k80pco4m0l1tcpvuv Usqp Cau




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円錐とは 体積 表面積の公式や求め方 受験辞典




中1数学 立体の体積と表面積 教科書p194 5 3学期期末テスト 赤城 ᐡᐤᐡ




角錐 円錐の体積と表面積の公式 数学fun




体積の求め方 計算公式一覧



6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積
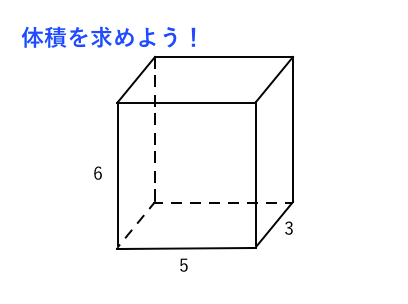



超簡単 体積の求め方 苦手な数学を簡単に




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の体積を求める公式




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4




小5 算数 小5 5 体積の求め方のくふう Youtube




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
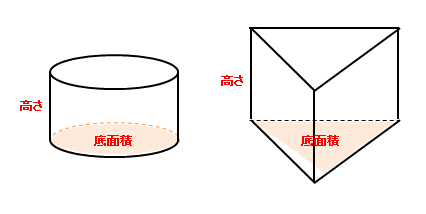



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




球の表面積と体積の公式 数学fun




球の表面積と体積の公式 数学fun




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



6年算数立体の体積1 教え方




中1数学 立体の表面積 例題編 映像授業のtry It トライイット




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



0 件のコメント:
コメントを投稿